Posts by Collection

We develop a finite element framework for the solution of stochastic elastoplastic boundary value problems with non-Gaussian parametric uncertainty. The framework relies upon a stochastic Galerkin formulation, where the stiffness random field is decomposed using a multidimensional polynomial chaos expansion. At the constitutive level, a Fokker-Planck-Kolmogorov (FPK) plasticity framework is utilized, under the assumption of small strain kinematics. A linearization procedure is developed that serves to update the polynomial chaos coefficients of the expanded random stiffness in the elastoplastic regime, leading to a nonlinear least-squares optimization problem. The proposed framework is illustrated in a static shear beam example of elastic-perfectly plastic as well as isotropic hardening material Read more

Quantifying the effect of reduced gravity on the behavior of granular matter is essential to understanding the evolution of planetary morphology, and will likely affect the design of future extraterrestrial habitats. Yet, despite recent research efforts, the effect of reduced gravity/confining pressure on strength remains undetermined with scarce results ranging from no effect to opposing trends. In this study we employ high-fidelity discrete element simulations (DEM) of passive failure experiments to measure the influence of gravity on the peak and steady state friction angle, and the angle of repose of sand. The results are compared against recently reported physical experiments, lending the latter support based on micromechanical information, that is unattainable experimentally. We find that the friction angles experience a small increase with decreasing gravity, while the angle of repose remains almost constant. Read more

A computational framework is developed for high-fidelity virtual (in silico) experiments on granular materials. By building on i) accurate mathematical representation of particle morphology and contact interaction, ii) full control of the initial state of the assembly, and iii) discrete element simulation of arbitrary stress paths, the proposed framework overcomes important limitations associated with conventional experiments and simulations. The framework is utilized to investigate the incremental response of sand through stress probing experiments, focusing on key aspects such as elasticity and reversibility, yielding and plastic flow, as well as hardening and fabric evolution. It is shown that reversible strain envelopes are contained within elastic envelopes during axisymmetric loading, the yield locus follows approximately the Lade-Duncan criterion, and the plastic flow rule exhibits complex nonassociativity and irregularity. Hardening processes are delineated by examining the stored plastic work and the fabric evolution in the strong and weak networks. Special attention is given to isolating in turn the effect of particle shape and interparticle friction on the macroscopic response. Interestingly, idealization of particle shape preserves qualitatively most aspects of material behavior… Read more

Dry granular systems respond to shear by a process of self-organization, that is nonlocal in nature. We study the interplay between the topological, kinematical and force signature of this process during shear banding in an sample of angular sand. Using Level-Set Discrete Element simulations of an in-situ triaxial compression experiment, and complex networks techniques, we identify communities of similar topology (cycles), kinematics (vortex clusters) and kinetics (force chains), and study their cooperative evolution. We conclude by discussing the implications of our observations for continuum modeling, including the identification of mesoscale order parameters, and the development of nonaffine kinematics models. Read more

We develop a Data-Driven framework for multiscale mechanical analysis of materials. The proposed framework relies on the Data-Driven formulation in mechanics, with the material data being directly extracted from lower-scale computations. Particular emphasis is placed on two key elements: the parametrization of material history, and the optimal sampling of the mechanical state space. We demonstrate an application of the framework in the prediction of the behavior of sand, a prototypical complex history-dependent material. In particular, the model is able to predict the material response under complex nonmonotonic loading paths, and compares well against plane strain and triaxial compression shear banding experiments. Read more

Nonlocal effects permeate most microstructured materials, including granular media, metals and foams. The quest for predictive nonlocal mechanical theories with well-defined internal length scales has been ongoing for more than a century since the seminal work of the Cosserats. We present here a novel framework for the nonlocal analysis of material behavior, which bypasses the need to define any internal length scale. This is achieved by extending the Data-Driven paradigm in mechanics, originally introduced for simple continua, into generalized continua. The problem is formulated directly on a material data set, comprised of higher-order kinematics and their conjugate kinetics, which are identified from experiments or inferred from lower scale computations. The case of a micropolar continuum is used as a vehicle to introduce the framework, which may also be adapted to strain-gradient and micromorphic media. Two applications are presented: a micropolar elastic plate with a hole, which is used to demonstrate the convergence properties of the method, and the shear banding problem of a triaxially compressed sample of quartz sand, which is used to demonstrate the applicability of the method in the case of complex history-dependent material behavior. Read more

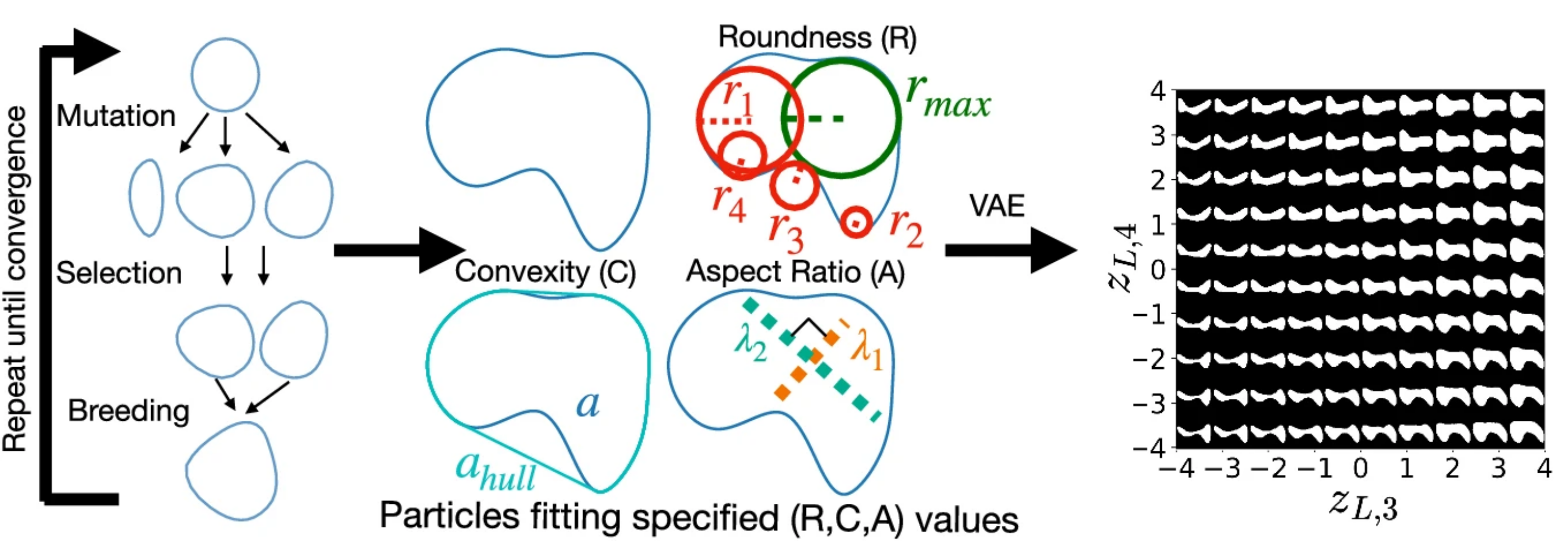
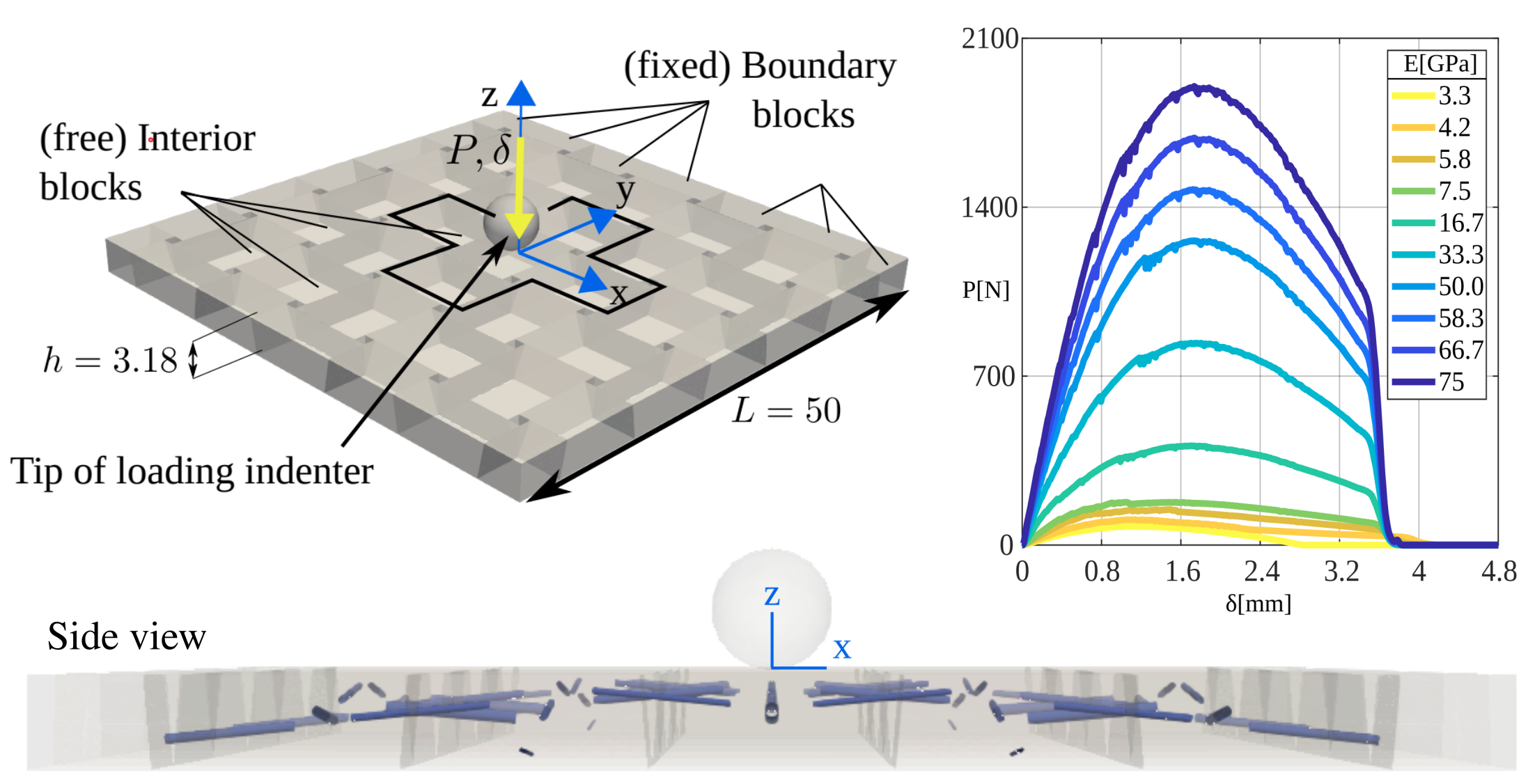
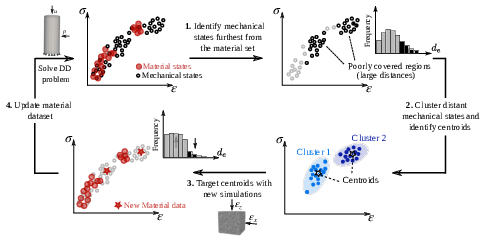
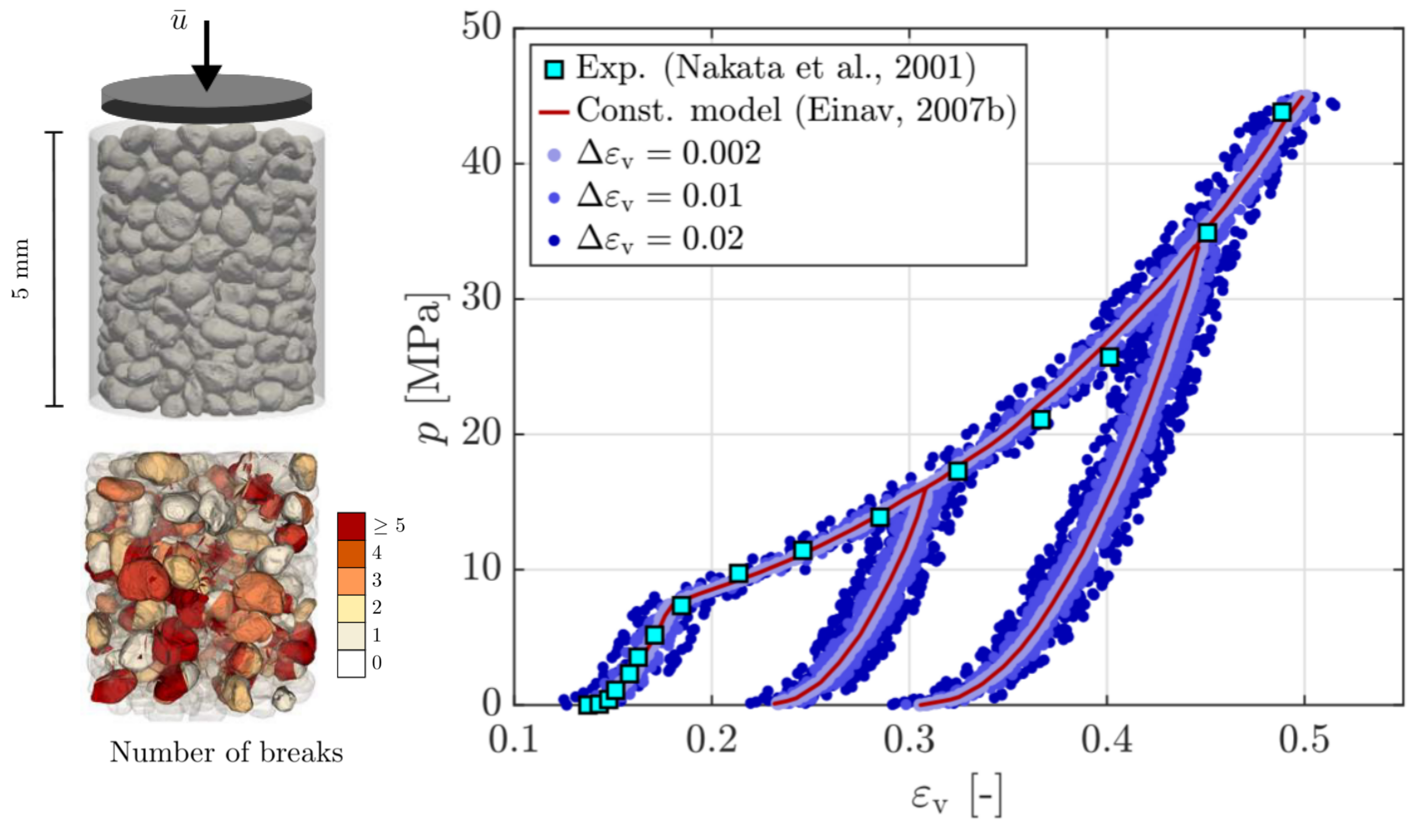
Under external perturbations, inter-particle forces in disordered granular media are well known to form a heterogeneous distribution with filamentary patterns. Better understanding these forces and the distribution is important for predicting the collective behavior of granular media, the media second only to water as the most manipulated material in global industry. However, studies in this regard so far have been largely confined to granular media exhibiting only geometric heterogeneity, leaving the dimension of mechanical heterogeneity a rather uncharted area. Here, through a FEM contact mechanics model, we show that a heterogeneous inter- particle force distribution can also emerge from the dimension of mechanical heterogeneity alone. Specifically, we numerically study inter-particle forces in packing of mechanically heterogeneous disks arranged over either a square or a hexagonal lattice and under quasi-static biaxial compression. Our results show that, at the system scale, a hexagonal packing exhibit a more heterogeneous inter-particle force distribution than a square packing does; At the particle scale, for both packing lattices, preliminary analysis shows the consistent coexistence of outliers (i.e., softer disks sustaining larger forces while stiffer disks sustaining smaller forces) in comparison to their homogeneous counterparts, which implies the existence of nonlocal effect. Further analysis on the portion of outliers and on spatial contact force correlations suggest that the hexagonal packing shows more pronounced nonlocal effect over the square packing under small mechanical heterogeneity. However, such trend is reversed when assemblies becomes more mechanically heterogeneous. Lastly, we confirm that, in the absence of particle reorganization events, contact friction merely plays the role of packing stabilization while its variation has little effect on inter-particle forces and their distribution. Read more

With increasingly advanced manufacturing techniques, architected materials or metamaterials continue to gain popularity. Yet, the vast majority of these materials are designed with a periodic and regular lattice structure. On the other hand, architected disordered materials have received little attention despite their robustness and flaw tolerance compared to regular lattice-based materials. The aim of the project D4M (Deform) is the development of a novel rational framework for data-driven, and hence experience-free, design of materials, that systematically exploits disorder. Read more

We study the transmission of compressive and tensile stresses, and the development of stress - induced anisotropy in entangled granular structures composed of nonconvex S-shaped hooks and staples. Utilizing discrete element simulations, we find that these systems exhibit fundamentally different behavior compared to standard convex particle systems, including the ability to entangle which contributes to a lower jamming packing fraction and facilitates the transmission of tensile stresses. We present direct evidence of tensile stress chains, and show that these chains are generally sparser, shorter and shorter-lived than the compressive chains found in convex particle packings. We finally study the probability distribution, angular density and anisotropic spatial correlation of the minor (compressive) and major (tensile) particle stresses. The insight gained for these systems can help the design of reconfigurable and recyclable granular structures capable of bearing considerable loads, without any need for reinforcement. Read more

Engineered granular materials have gained considerable interest in recent years. For this substance, the primary design variable is grain shape. Optimizing grain form to achieve a macroscopic property is difficult due to the infinite-dimensional function space particle shape inhabits. Nonetheless, by parameterizing morphology the dimension of the problem can be reduced. In this work, we study the effects of both intuitive and machine-picked shape descriptors on granular material properties. First, we investigate the effect of classical shape descriptors (roundness, convexity, and aspect ratio) on packing fraction 𝜙 and coordination number Z. We use a genetic algorithm to generate a uniform sampling of shapes across these three shape parameters. The shapes are then simulated in the level set discrete element method. We discover that both 𝜙 and Z decrease with decreasing convexity, and Z increases with decreasing aspect ratio across the large sampling of morphologies—including among highly non-convex grains not commonly found in nature. Further, we find that subtle changes in mesoscopic properties can be attributed to a continuum of geometric phenomena, including tessellation, hexagonal packing, nematic order and arching. Nonetheless, such descriptors alone can not entirely describe a shape. Thus, we find a set of 20 descriptors which uniquely define a morphology via deep generative models. We show how two of these machine-derived parameters affect 𝜙 and Z. This methodology can be leveraged for topology optimization of granular materials, with applications ranging from robotic grippers to materials with tunable mechanical properties. Read more

Topological Interlocking Structures (TIS) are assemblies of interlocking building blocks that hold together solely through contact and friction at the blocks’ interfaces, and thus do not require any connective elements. This salient feature makes them highly energy-absorbing, resistant to crack propagation, geometrically versatile, and re-usable. It also gives rise to failure mechanisms that, differently from ordinary structures, are governed by multiple contact interactions between blocks and frictional slip at their interfaces. Commonly-used modeling tools for structural analysis severely struggle to capture and quantify these unusual failure mechanisms. Here, we propose a different approach that is well suited to model the complex failure of TIS. It is based on the Level-Set-Discrete-Element-Method, originally developed for granular mechanics applications. After introducing the basic assumptions and theoretical concepts underlying our model, we show that it well-captures experimentally observed slip-governed failure in TIS slabs and that it estimates the force-displacement curves better than presently available modeling tools. The theoretical foundation together with the results of this study provide a proof-of-concept for our new approach and point to its potential to improve our ability to model and to understand the behavior of interlocked structural forms. Read more

Data-Driven (DD) computing is an emerging field of Computational Mechanics, motivated by recent technological advances in experimental measurements, the development of highly predictive computational models, advances in data storage and data processing, which enable the transition from a material data-scarce to a material data-rich era. The predictive capability of DD simulations is contingent on the quality of the material data set, i.e. its ability to closely sample all the strain-stress states in the phase space of a given mechanical problem. In this study, we develop a methodology for increasing the quality of an existing material data set through iterative expansions. Leveraging the formulation of the problems treated with the DD paradigm as distance minimization problems, we identify, using unsupervised learning, regions in phase space with poor data coverage, and target them with additional experiments or lower-scale simulations. The DD solution informs the additional experiments so that they can provide better coverage of the phase space of a given application. We first illustrate the convergence properties of the approach through a DD finite element simulation of a linear elastic cylinder under triaxial compression. The same numerical experiment is then performed on a specimen of Hostun sand, a material with complex history-dependent behavior. Data sampling is performed with Level-Set Discrete Element Method (LS-DEM) calculations of unit cells representative of this granular material, subjected to loading paths determined by the proposed method. It is shown that this adaptive expansion of the data set, tailored for a particular application, leads to convergent and accurate DD predictions, without the computational cost of using large databases with potentially redundant or low-quality data Read more

This paper presents a model-free data-driven framework for breakage mechanics. In contrast with continuum breakage mechanics, the de facto approach for the macroscopic analysis of crushable granular media, the present work bypasses the need for constitutive models and phenomenological assumptions, relying on material behavior that is known only through empirical data. For this purpose, we revisit the recent developments in model-free data-driven computing for history-dependent materials and extend the main ideas to materials with particle breakage. A systematic construction of the modeling framework is presented, starting from the closed-form representation of continuum breakage mechanics and arriving at alternative model-free representations. Simulations of a real experimental test in crushable sand are conducted, where the data is furnished by lower-scale simulations, indicating that the proposed framework is able to accurately predict the mechanics of crushable materials including the state of comminution. Read more

A class of irregular cellular materials with engineered topological and geometrical disorder is introduced, which represents a shift from conventional periodic lattice designs. We first develop a graph learning model for predicting the fracture path in these architected materials. The model employs a graph convolution for spatial message passing, and a gated recurrent unit architecture for temporal dependence. Once trained on data gleaned from experimentally validated elastoplastic beam finite element analyses, the learned model produces accurate predictions overcoming the need for expensive finite element calculations. We finally leverage the trained model in combination with a downstream optimization scheme to generate optimal architectures that maximize the crack path length and, hence, the associated fracture energy. Read more

This is a description of your talk, which is a markdown files that can be all markdown-ified like any other post. Yay markdown! Read more

Read more

Read more

Read more

Read more

Read more

Read more