Adaptive Goal-oriented Data Sampling in Data-Driven Computational Mechanics
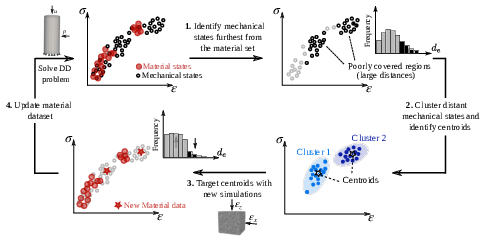Data-Driven (DD) computing is an emerging field of Computational Mechanics, motivated by recent technological advances in experimental measurements, the development of highly predictive computational models, advances in data storage and data processing, which enable the transition from a material data-scarce to a material data-rich era. The predictive capability of DD simulations is contingent on the quality of the material data set, i.e. its ability to closely sample all the strain-stress states in the phase space of a given mechanical problem. In this study, we develop a methodology for increasing the quality of an existing material data set through iterative expansions. Leveraging the formulation of the problems treated with the DD paradigm as distance minimization problems, we identify, using unsupervised learning, regions in phase space with poor data coverage, and target them with additional experiments or lower-scale simulations. The DD solution informs the additional experiments so that they can provide better coverage of the phase space of a given application. We first illustrate the convergence properties of the approach through a DD finite element simulation of a linear elastic cylinder under triaxial compression. The same numerical experiment is then performed on a specimen of Hostun sand, a material with complex history-dependent behavior. Data sampling is performed with Level-Set Discrete Element Method (LS-DEM) calculations of unit cells representative of this granular material, subjected to loading paths determined by the proposed method. It is shown that this adaptive expansion of the data set, tailored for a particular application, leads to convergent and accurate DD predictions, without the computational cost of using large databases with potentially redundant or low-quality data 