Data-Driven Nonlocal Mechanics
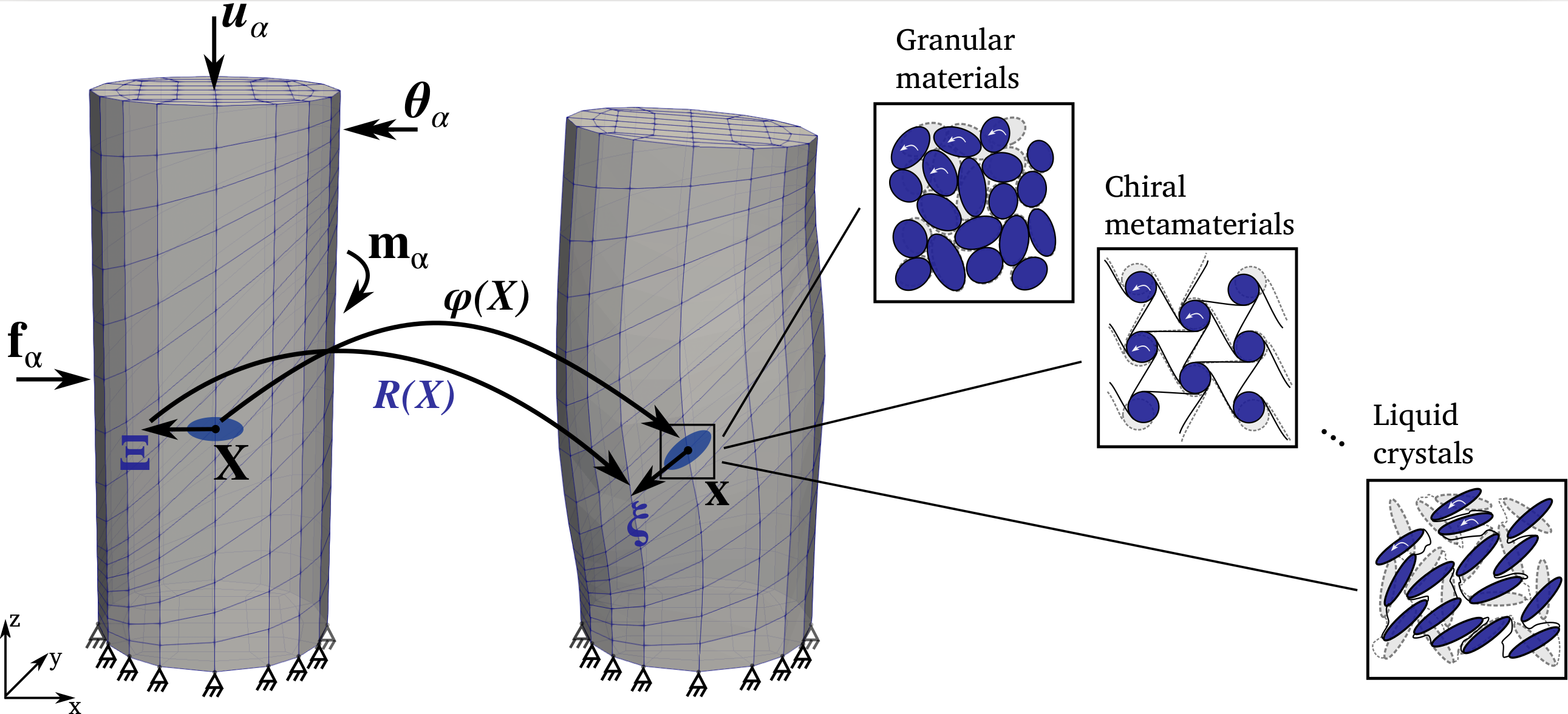Nonlocal effects permeate most microstructured materials, including granular media, metals and foams. The quest for predictive nonlocal mechanical theories with well-defined internal length scales has been ongoing for more than a century since the seminal work of the Cosserats. We present here a novel framework for the nonlocal analysis of material behavior, which bypasses the need to define any internal length scale. This is achieved by extending the Data-Driven paradigm in mechanics, originally introduced for simple continua, into generalized continua. The problem is formulated directly on a material data set, comprised of higher-order kinematics and their conjugate kinetics, which are identified from experiments or inferred from lower scale computations. The case of a micropolar continuum is used as a vehicle to introduce the framework, which may also be adapted to strain-gradient and micromorphic media. Two applications are presented: a micropolar elastic plate with a hole, which is used to demonstrate the convergence properties of the method, and the shear banding problem of a triaxially compressed sample of quartz sand, which is used to demonstrate the applicability of the method in the case of complex history-dependent material behavior. 